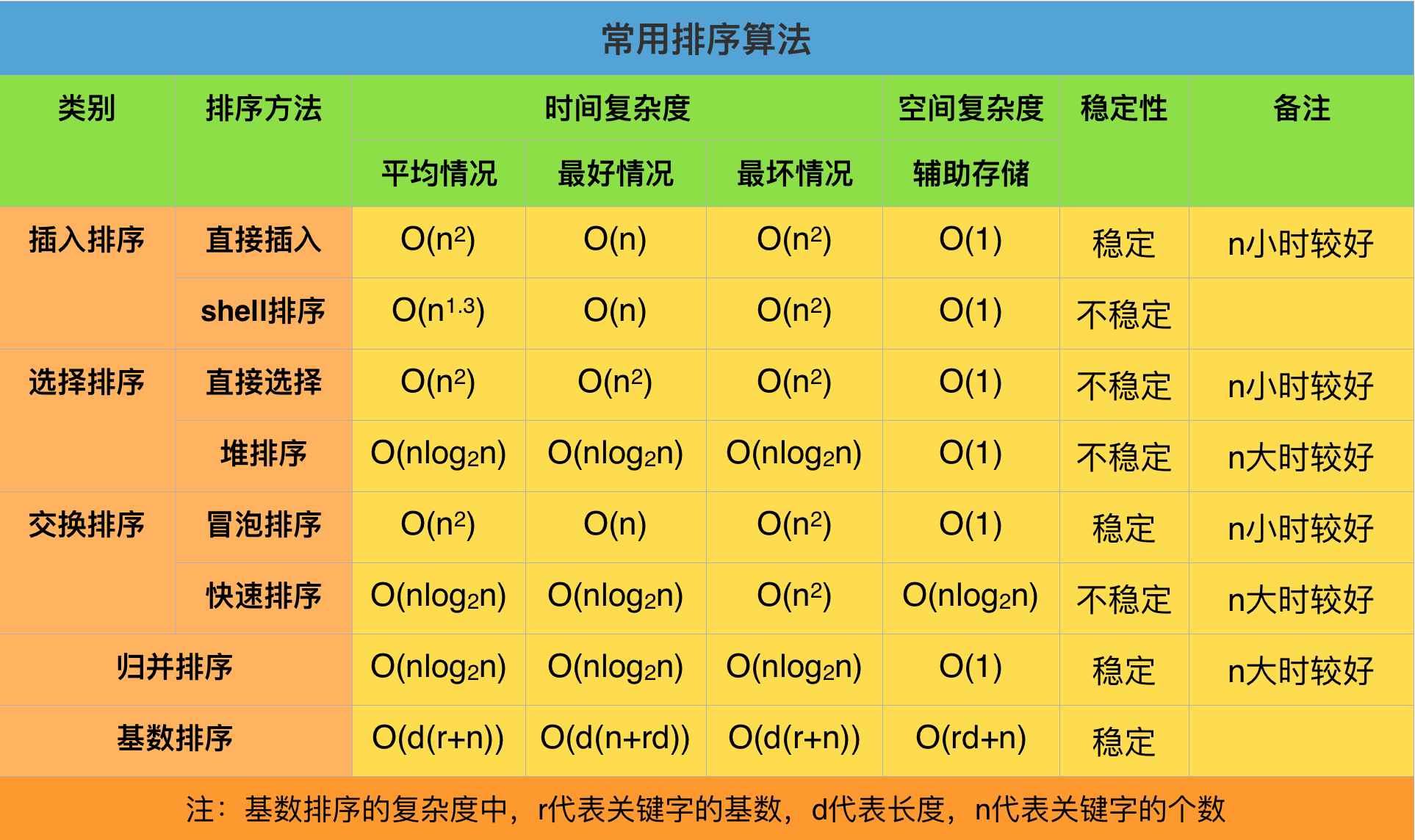
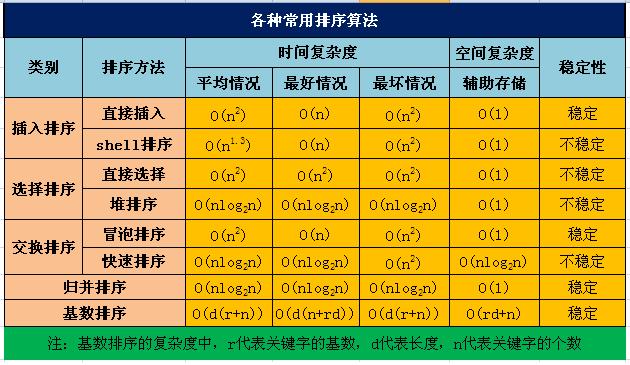
总结一些常用的排序算法,如冒泡排序、插入排序、快速排序、计数排序、二分排序、归并排序等。
Source
冒泡排序
伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
function bubble_sort (array, length) {
var i, j;
for(i from 0 to length-1){
for(j from 0 to length-1-i){
if (array[j] > array[j+1])
swap(array[j], array[j+1])
}
}
}
函数 冒泡排序 输入 一个数组名称为array 其长度为length
i 从 0 到 (length - 1)
j 从 0 到 (length - 1 - i)
如果 array[j] > array[j + 1]
交换 array[j] 和 array[j + 1] 的值
如果结束
j循环结束
i循环结束
函数结束
|
python实现
1
2
3
4
5
6
|
def bubble(List):
for j in range(len(List)-1,0,-1):
for i in range(0, j):
if List[i] > List[i+1]:
List[i], List[i+1] = List[i+1], List[i]
return List
|
插入排序
python实现
1
2
3
4
5
6
7
|
def insert_sort(lst):
n=len(lst)
if n==1: return lst
for i in range(1,n):
for j in range(i,0,-1):
if lst[j] < lst[j-1]: lst[j], lst[j-1] = lst[j-1], lst[j]
return lst
|
快速排序
python实现
1
2
3
4
5
6
|
def quicksort(a):
if len(a) == 1:
return a[0]
if len(a) < 1:
return 0
return quicksort([x for x in a[1:] if x < a[0]]), [a[0]], quicksort([x for x in a[1:] if x > a[0]])
|
C语言实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
int partition(int arr[], int low, int high){
int key;
key = arr[low];
while(low < high){
while(low < high && arr[high]>= key )
high--;
if(low < high)
arr[low++] = arr[high];
while( low < high && arr[low]<=key )
low++;
if(low < high)
arr[high--] = arr[low];
}
arr[low] = key;
return low;
}
void quick_sort(int arr[], int start, int end){
int pos;
if (start < end){
pos = partition(arr, start, end);
quick_sort(arr,start,pos-1);
quick_sort(arr,pos+1,end);
}
return;
}
|
归并排序
python实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
from collections import deque
def merge_sort(lst):
if len(lst) <= 1:
return lst
def merge(left, right):
merged,left,right = deque(),deque(left),deque(right)
while left and right:
merged.append(left.popleft() if left[0] <= right[0] else right.popleft()) # deque popleft is also O(1)
merged.extend(right if right else left)
return list(merged)
middle = int(len(lst) // 2)
left = merge_sort(lst[:middle])
right = merge_sort(lst[middle:])
return merge(left, right)
|
计数排序
C实现
1
2
3
4
5
6
7
8
9
10
11
12
13
|
void counting_sort(int *ini_arr, int *sorted_arr, int n) {
int *count_arr = (int *) malloc(sizeof(int) * 100);
int i, j, k;
for (k = 0; k < 100; k++)
count_arr[k] = 0;
for (i = 0; i < n; i++)
count_arr[ini_arr[i]]++;
for (k = 1; k < 100; k++)
count_arr[k] += count_arr[k - 1];
for (j = n; j > 0; j--)
sorted_arr[--count_arr[ini_arr[j - 1]]] = ini_arr[j - 1];
free(count_arr);
}
|
二分查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
int binary_search(int array[],int n,int value){
int left=0;
int right=n-1;
while (left<=right){
int middle=left + ((right-left)>>1); //防止溢出,移位也更高效。同时,每次循环都需要更新。
if (array[middle] > value) {
right =middle-1;
}
else if(array[middle] < value) {
left=middle+1;
}
else {
return middle;
}
}
return -1;
}
|